锂电池分数阶建模与荷电状态估计研究

来源 | 《电源技术》杂志

导读：基于分数阶微积分理论及实际电容在本质上是分数阶的事实，整数阶建模会导致算法不精确。因此，针对这一问题，建立锂电池分数阶PNGV等效电路模型并进行理论分析，通过混合脉冲功率特性实验（HPPC)对模型参数进行辨识。

能源危机和环境污染问题日益成为话题，新能源汽车正在逐步替代传统能源汽车。锂离子电池（简称锂电池）因其比能量高、携带方便、寿命周期长等优点被广泛应用于电动汽车及混合动力汽车上[1]。电池管理系统（BMS）的主要功能是确保系统的优化性能和安全运行，其中荷电状态（SOC）估计是其最重要的任务，实时SOC估计是实现剩余行驶里程预测的关键技术之一[2]。

锂电池是一个复杂的化学系统[3]，由于其内部状态无法直接测量，因此需要对此进行建模。常见的电池模型有电化学模型和等效电路模型[4]。文献[5]以锂电池电化学方程为基础，建立锂电池电化学模型并确定电池参数，但电化学模型所涉及的方程数和参数较多，计算冗余且难以获取。实际电路中的电容仅仅是趋于整数阶，但在本质上是分数阶的，并且从电化学的角度揭示了动力电池的分数阶本质。文献[6-7]建立了基于二阶等效电路的分数阶电池模型，并采用遗传算法进行参数化，最后利用FOKF算法估算电池SOC。文献[8]采用一阶戴维南（Thevenin）模型结合安时法建立电池模型，并采用平方根采样点卡尔曼滤波实现对电池等效模型参数的辨识及对电池荷电状态的估算。但上述两种锂电池模型的精度不高，且存在发散的可能。

充分考虑到锂电池内部的电化学反应过程所引起很强的非线性和不确定性，本文基于Grunwald-Latnikov(G-L)分数阶微积分定义提出了锂电池分数阶PNGV模型，该模型在不降低模型精度的前提下，不仅简化了模型结构，而且减少了计算量。并通过HPPC实验对模型中各参数进行辨识，通过对实验曲线进行对比辨识阶数，针对所建模型设计并仿真FOKF算法估计电池SOC，通过恒流放电实验证明，运用FOKF算法估计SOC在跟踪速度和精度上较UKF有了提高，具备工程应用价值。

1、锂电池分数阶PNGV等效模型建立

1.1 分数阶建模

电池SOC的精确估算需要建立准确的等效电路模型。考虑到电池模型既要较好地描述电池的极化效应和充放电特性，又不能过于复杂，且能便于工程应用，也考虑到分数阶微积分在描述电池等非线性系统方面具有准确性高的特点，本文基于分数阶微积分理论提出了分数阶PNGV模型。

锂电池PNGV模型于2001年在美国新一代汽车合作计划中被提出，其包括一阶电阻电容（RC）模块，为一阶RC模型，是电池非线性模型中的典型代表。PNGV的模型如图1所示。

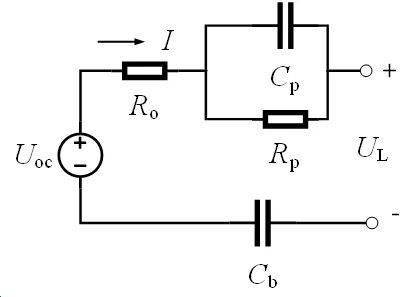
图1 PNGV锂电池等效电路模型

图1中，Uoc为开路电压，当SOC减少时，Uoc也会跟着下降；RO为欧姆内阻；储能电容Cb描述充放电电流变化时累积产生的开路电压的变化；RP和CP分别表征电池的极化内阻和极化电容，二者并联，模拟电池的极化效应；UL为端电压，I为工作电流。其中，极化电容CP和电容Cb可以用分数阶表示为：

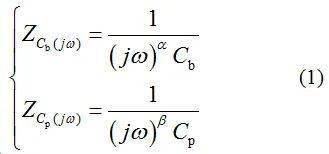
式中： a、b分别为储能电容Cb和极化电容CP的分数阶阶数， 0≤a≤1，0≤b≤1。

根据图1所示的模型和戴维南定理可得：

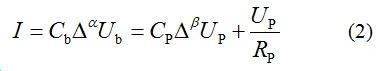
基于分数阶模型的状态空间方程可描述为：

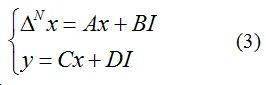
式中：

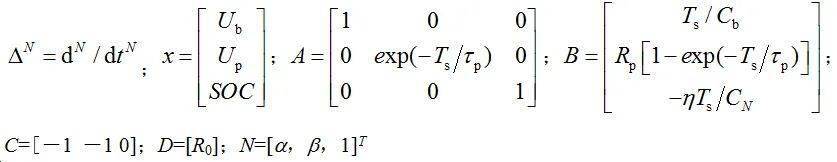
式中：Ub为电容Cb两端电压，UP为电容CP两端电压；y为系统的测量值，UL为电池充放电过程中的端电压值；CN为电池的额定容量； h=0.98，表示电池的充放电效率；Ts为系统采样周期，本文中Ts取1 s；时间常数 t= R P C P ，其大小反映了一阶电路过渡过程进展速度，是反映过渡过程特性的重要的量[9]。

本文引入分数阶微积分，G-L定义是广泛使用的一种分数阶微积分定义形式，其数学表达式为：

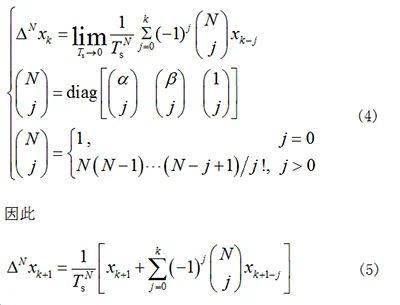
根据所选定的锂电池模型，将其根据随机理论离散化，将电流值作为系统的输入，电压值作为系统的输出，SOC作为系统的一个状态变量，基于G-L定义锂电池PNGV分数阶模型的状态空间离散方程和测量方程为：

式中：xk、xk+1分别为k时刻、k＋1时刻x的状态变量；wk、vk分别为系统的过程噪声和测量噪声，他们都是期望为零的高斯白噪声。

1.2 模型参数辨识

模型参数辨识实验仿照《FreedomCAR电池实验手册》中的HPPC实验，本文以松下NCR18650B锂电池为例，其标称电压为3.7 V，标称容量为3 400 mAh，在室温下以4.8 A的恒流放电和3.6 A的恒流充电进行实验，并且在每完成一次实验后，对电池进行3.6 A的恒流放电使电池模块SOC值降为90%，80%，…，0，循环执行实验并记录，得到不同SOC值下的各参数值，如表1所示。

表1 不同SOC状态下的模型辨识参数

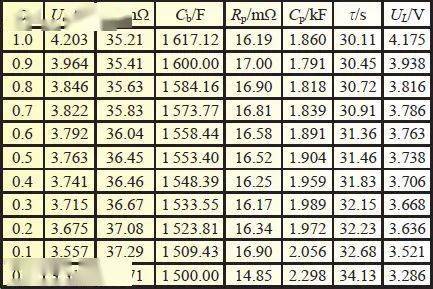
在MATLAB中使用具有最小二乘法拟合意义的polyfit函数将表1中Uoc和SOC关系采用5次拟合表示，如图2所示。

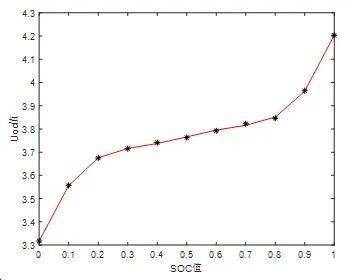
图2 Uoc与SOC的关系曲线

其表达式为：

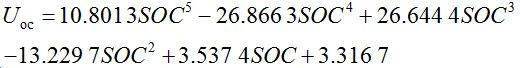
1.3 仿真模型的建立与分析

本文在Matlab/Simulink中建立了如图3的仿真框图[10]，其中子模块以电容阶数为0.8为例，如图3（b）所示。图3是以SOC=1为例，将真实的Uoc值和脉冲电流值，及通过模型辨识所求取的各参数作为输入，得到电容的阶数分别在整数阶、0.8阶和0.9阶时仿真模型的输出UL值，将其与实验输出的UL值进行比较。

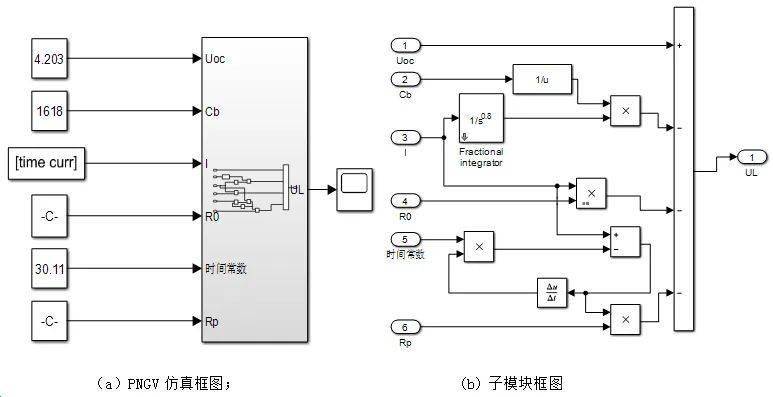
图3 锂电池PNGV仿真模型

本文通过HPPC放电工况对模型进行仿真。[0 s，10 s]内无电流通过，[10 s，20 s]内放电电流为4.8 A，[20 s，60 s]内断流，[60 s，70 s]内充电电流为3.6 A。图4所示为HPPC放电工况下整数阶模型、0.8阶模型、0.9阶模型仿真值和实验值的曲线比较。

图4 HPPC放电工况下的端电压波形

从图4中可见，在[10 s，20 s]内，整数阶模型中的UL值下降得更快，而0.8阶模型和0.9阶模型考虑到电容是一种分数阶元件而UL值下降得较缓，与真实的实验值更接近。而且，从图4中可以细微地看出，0.8阶模型和0.9阶模型在[10 s，20 s]内不是一条直线，而是一条曲线，更好地模拟电池在放电过程产生的极化效应对电压的影响。在[20 s，60 s]区间内，曲线都会因为电池内部存在极化效应，在断流的瞬间电压极速上升后再缓慢上升。从图4中，可以很清晰地得到整数阶与实验值的差值大于分数阶与实验值的差值，其中，0.9阶曲线比0.8阶曲线更接近于实验曲线，说明电容的阶数在[0.8，0.9]区间内，且更接近于0.9阶，取阶数为0.88。因此，建立分数阶的电池PNGV模型是合理的，而且更精确地反映电池的充放电特性。

2、基于分数阶卡尔曼滤波算法估计SOC

2.1 本文构造的分数阶卡尔曼滤波[11]

(1) 确定状态变量的初始值和初始协方差矩阵P0：

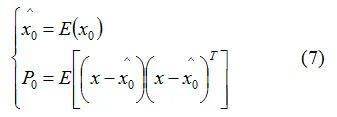
(2) 由k－1时刻的状态和误差协方差矩阵对k时刻的状态和误差协方差矩阵进行时间更新：

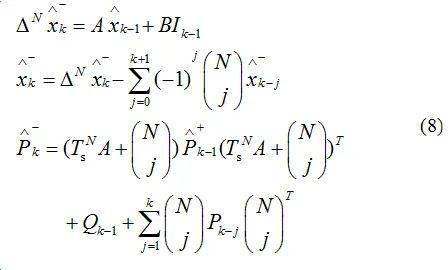
(3) 卡尔曼增益矩阵Kk为：

(4) 用k时刻的测量输出值对状态和误差协方差矩阵进行测量更新，获得更准确的估计结果：

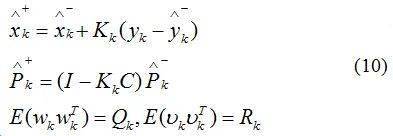
2.2 仿真实验

为了验证分数阶滤波算法的精度和有效性，在Matlab/Simulink中，以18650B型锂电池为例，设计工况下的放电实验。将该电池进行0.5 C的恒流充电，当电池电压达到上限电压4.3 V时换为恒压充电，直到充电倍率减小到0.05 C认为电池电量已满，这时SOC值为1，静置24 h。仿真环境和实验环境都是以1 A的放电电流放电,那么FOKF和无迹卡尔曼滤波（UKF）在相同的状态协方差初值和测量协方差初值下得到脉冲放电工况下的滤波曲线。

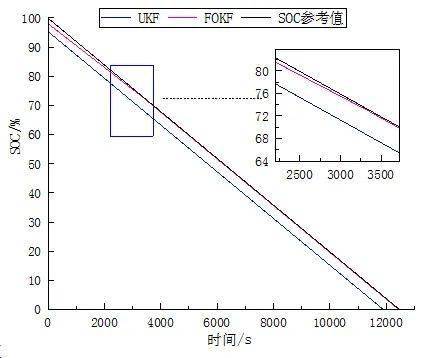
图5 恒流放电下，SOC参考值与FOKF、UKF算法估计值对比

由图5可知，一方面，基于模型的UKF算法和FOKF算法均能快速跟踪SOC参考值，但FOKF比UKF跟踪速度更快；另一方面，精度定义为仿真稳定输出值与参考值的误差，FOKF的估计值的绝对误差保持在2%以内，较UKF算法的绝对误差5%有了一定的提高。

结 语

本文根据锂电池的工作模式，将分数阶微积分理论应用到电池建模和荷电状态估计中，提出了基于分数阶PNGV锂电池模型的SOC估计方法，通过实验和仿真估计，所得如下结论：（1）基于锂电池的极化效应与电池内部动态特性，建立分数阶PNGV模型，并通过HPPC实验求取PNGV模型的各个参数。根据在Matlab/Simulink建立整数阶PNGV模型和分数阶PNGV模型，仿真输出的电池端电压UL值与实验所得的端电压UL值进行比较，表明建立的分数阶模型更精确，其中0.9阶模型的误差率小于0.2%，基本与实验值拟合，因此将阶数取为0.88；（2）基于所建立的模型，建立离散状态方程和测量方程，利用FOKF算法估计电池SOC，并与UKF算法和SOC参考值进行比较，结果表明FOKF算法估计SOC跟踪速度更快，绝对误差在2%以内，准确度更高。

参考文献:

[1] WANG Y, ZHANG C, CHEN Z.A method for state-of-charge estimation of LiFePO4 batteries at dynamic currents and temperatures using particle fifilter[J]. Journal of Power Sources, 2015, 279: 306-311.

[3] MASTALI M, VAZQUEZ-ARENAS J, FRASER R. Battery state of the charge estimation using Kalman fifiltering[J]. Journal of Power Sources, 2013, 239: 294-307.

[4] CHIANG Y, SEAN W, KE J C.Online estimation of internal resistance and open-circuit voltage of

[5] 杨俊，张希，高一钊.锂电池电化学传递函数模型建模及参数辨识[J].电源技术，2019，43(7)：1132-1135.

[7] 刘树林，崔纳新，李岩，等.基于分数阶理论的车用锂离子电池建模及荷电状态估计[J].电工技术学报，2017，32(4)：189-195.

[9] 梁奇，于春梅，王顺利，等．基于PNGV电路模型的航空钴酸锂电池内阻研究[J]．电源学报，2017，15(2)：153-158.

[11] 鲁伟，续丹，杨晴霞，等.锂电池分数阶建模与荷电状态研究[J].西安交通大学学报，2017，51(7)：124-129.

作者：李 静，杨 艳，秦建鑫，赵亚洲，周万鹏

单位：青岛大学 电气工程学院